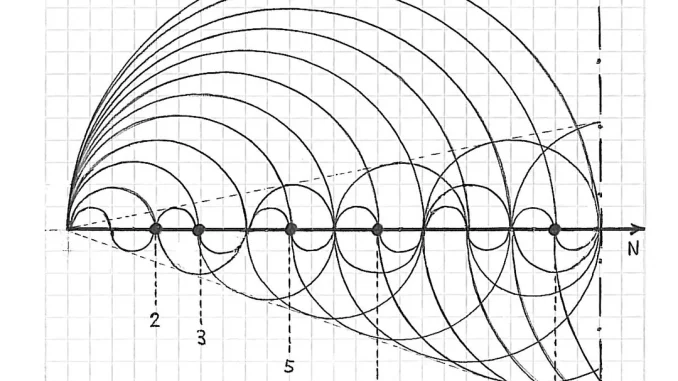
Το ακόλουθο άρθρο δημοσιεύθηκε στις 16/09/2005 σε κάποιο παλιό ελληνικό μπλογκ για τα μαθηματικά (δυστυχώς δεν υπάρχει πια)
Παρασκευή, Σεπτέμβριος 16, 2005
Οι πρώτοι αριθμοί
“Κουδούνι ρε στούρνοι, μαζευτείτε στην τάξη. Τσιμπουκίδου σβήσε το τσιγάρο τώρα. Και πηγαίντε και μαζεύτε τον Μπάμπη το Σουγιά απο τις σκάλες, πάλι μαστούρωσε ο καμμένος”
“Μα κύριε καθηγητά..”
“Κεριά να σας μπούν εκεί που δεν μπαίνει φώς ρε!. Παλουκωθείτε”
“αχ πως τα λέτε κύριε καθηγητα…”
“Τσιμπουκίδου εσένα στο μπουλκουμέ ο νους σου. Χρειάζεσαι χρειαζεσαι ιδιαίτερα.. μανούλι..
Λοιπόν σήμερα αγαπητά μου ζώα, θα σας μιλήσω για τους πρώτους αριθμούς. Τους έχετε ακουστά ή ..
“Ε ναι κυριε καθηγητα, 1,2,3,4,5 αυτοι είναι οι πρώτοι”
“Τον κακό σου το φλάρο. Σκάστε και ακούστε ..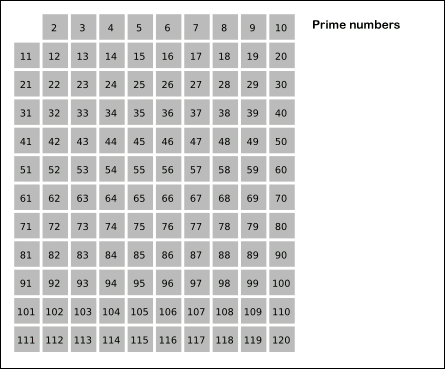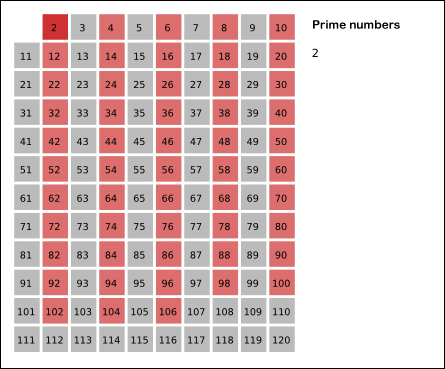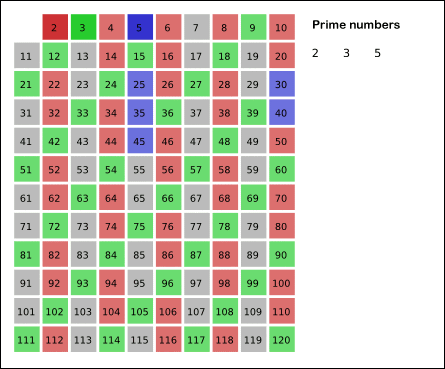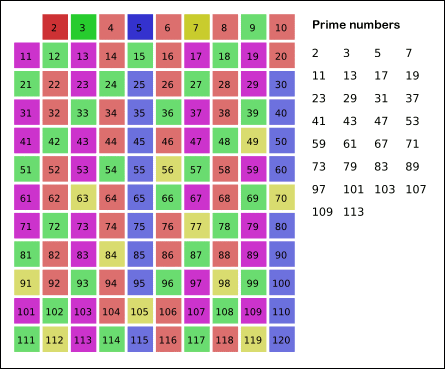
Πρώτος ονομάζεται κάθε φυσικός αριθμός, μεγαλύτερος του 1 που μόνοι του θετικοί διαιρέτες είναι το 1 και ο εαυτός του. Οι άλλοι αριθμοί ονομάζονται σύνθετοι. Καταφέρατε να μπερδευτείτε ε?
Ποιοί είναι οι φυσικοί αριθμοί Στουρναρίδη?
“Οι θετικοί ακέραιοι κύριε καθηγητά : 0,1,2,3,4,5,6… κλπ”
“!!!!!! Στουρναρίδη παίρνεις αναβολικά? 🙂 🙂 »
Ετσι.. πουχου : Το 5 είναι πρώτος αριθμός γιατί διαιρείται ακριβώς μόνο με τον εαυτό του και το 1.
Το ίδιο και το 7, το 11 κλπ..
Οι πρώτοι “πρώτοι” αριθμοί είναι οι εξής:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103…
Το 2 είναι ο μοναδικός ζυγός πρώτος αριθμός. Όπως θα παρατηρούσατε άμα δεν είχατε το μυαλό σας στα βυζιά της Τσιμπουκίδου, όλοι οι πρώτοι είναι μονοί, ή όπως θα λέγαμε εμείς οι μαθηματικοί, περιττοί.
Οι πρώτοι αριθμοί παιδεύουν τον κλάδο εδώ και χιλιάδες χρόνια, βασικά εξαιτίας του Θεμελιώδους θεωρήματος της αριθμητικής (που πρώτος απέδειξε ουσιαστικά ο Ευκλείδης), που λέει ότι Kάθε φυσικός αριθμός μπορεί να γραφεί σαν γινόμενο πρώτων αριθμών, και μάλιστα κατά μοναδικό τρόπο. Δηλαδή ζώα, ο οποιοσδήποτε θετικός ακέραιος αριθμός έχει μια μονοσήμαντη ανάλυση σε γινόμενο πρώτων αριθμών. Αυτό μπορεί να σας φαίνεται μπούρδα, αλλά έχει τρελλή εφαρμογή στον τομέα της κρυπτογραφίας.
Πως ? Ας πούμε οτι στέλνετε ένα κωδικοποιημένο μήνυμα σε έναν φίλο σας. Το κλειδί για την κωδικοποίηση είναι ένας πολύ πολύ μεγάλος αριθμός. Για να διαβάσει το μήνυμα ο τυπάς πρέπει να ξέρει την μονοσήμαντη ανάλυσή του σε πρώτους αριθμούς. Οποιοσδήποτε ήθελε να υποκλέψει το μήνυμα, του ήταν άχρηστο, γιατί για πολύ μεγάλους αριθμούς, η μονοσήμαντη ανάλυση σε πρώτους είναι μεγάαααλη ιστορία. Τώρα με τα πισιά έχουμε κάνει προόδους, αλλά και πάλι χρησιμοποιείται αυτή η μέθοδος, με αριθμούς μεγαλύτερους όμως του 10^100 αν θυμάμαι καλά. (αυτό είναι ένα 1 με 100 μηδενικά δίπλα ζώα…)
Το θεώρημα αυτό προφανώς δεν λαμβάνει υπόψην το 1 ως πρώτο γιατί θα είχαμε επιπλοκές που δεν είναι της ώρας να πούμε.
Θέμα δεύτερον : Υπάρχουν άπειροι πρώτοι αριθμοί.
Και αυτό ο Ευκλείδης το είπε ρε ζώα. Και το απέδειξε μάλλον, δεν το κατέβασε απλά απο τη γκλάβα του μια μέρα που έκανε μπουγάδα τις λερωμένες του χλαμύδες!
Και ξέρετε πως το απέδειξε? Με μια πολύ απλή σκέψη:
“Πάρτε πεπερασμένο αριθμό πρώτων. Πολλαπλασιάστε τους και προσθέστε ένα. Το νούμερο που βγαίνει ως αποτέλεσμα, δεν διαιρείται με κανέναν από το πεπερασμένο σύνολο των πρώτων, επειδή τότε πάντα θα είχαμε υπόλοιπο 1. Άρα είτε ο αριθμός αυτός είναι πρώτος, είτε διαιρείται από έναν άλλο πρώτο που δεν υπάρχει μέσα σε αυτό το σύνολο. Άρα έχουμε και άλλους πρώτους πέραν αυτού του συνόλου”
Σε αντίθεση με αυτό που θα υποψιαζόσασταν αν είχατε τα μυαλά σας στο μάθημα, το να βρούμε πρώτους αριθμούς, δεν είναι και τόσο εύκολο. Δεν έχουν έναν συγκεκριμένο ρυθμό ή τρόπο που εμφανίζονται. Είναι πιο εύκολο να τσεκάρουμε αν ένας αριθμός είναι πρώτος, παρά να βρούμε πρώτους αριθμούς. Ένας κλασσικός τρόπος για να ελέγξουμε αν ένας αριθμός είναι πρώτος, είναι το λεγόμενο “Κόσκινο του Ερατοσθένη”, αλλά σας βλέπω να νυστάζετε και το αφήνω για αύριο.
Δεν υπάρχει κάποιος τύπος για να βρίσκουμε πρώτους. Υπάρχει ο τύπος f(n)=n^2-n+41 αλλά μας δίνει πρώτους για n απο 0 μέχρι 40. Το f(41) δεν είναι πρώτος.
Η ιστορία με τους πρώτους είναι τεράστια και μπορεί να γεμίσει εγκυκλοπαίδειες ολοκληρες.
Γενιές και γενιές μαθηματικών έχουν σπάσει τα ξεράδια τους με αυτούς.
Τους έχουν χωρίσει και σε είδη κιόλας.
Υπάρχουν οι πρώτοι του Fermat : Πρώτοι που έχουν τη μορφή 2^(2^n) + 1
Οι πρώτοι του Mersenne : (2^n)-1
Οι πρώτοι του Wilson : Ένας πρώτος p είναι πρώτος του Wilson αν το p^2 διαιρεί το (p-1)!+1 κ.ο.κ
Θα μπορούσαμε να γράφουμε χιλιάδες σελίδων και να μην τελειώνουμε ποτέ..
Κλείνω το σημερινό μάθημα με τρία “ανοιχτά προβλήματα” που αφορούν πρώτους :
1. Η υπόθεση του Riemann : Ο Riemann μια μέρα, αφού είχε ξυπνήσει και είχε ρίξει έναν πρωινό στην υπηρέτριά του, είπε την αττάκα “χμμμ, οι πρώτοι πρέπει να είναι τοποθετημένοι όσο κανονικότερα γίνεται για την περίπτωσή τους” .
2. Η εικασία του Goldbach (που το ομότιτλο βιβλίο διάβασε όλη η Ελλάδα και προσπαθούν να το αποδείξουν απο φοιτήτριες της Φιλοσοφικής μεχρι του παιδαγωγικού..ελεος) : Κάθε ακέραιος μεγαλύτερος του 2 μπορεί να γραφεί ως άθροισμα πρώτων?
3. Η εικασία του Legendre (ευτυχώς που δεν έχει κυκλοφορήσει στους κύκλους των βιβλιόφιλων γιατί πάλι θα με έπαιρναν τηλέφωνο στις 4 το πρωί να με ρωτήσουν παπατζιλίκια, όπως με τον Goldbach) : Για κάθε n υπάρχει πρώτος αριθμός μεταξύ των n^2 και (n+1)^2
Αγαπητά μου παιδιά, κατ’ αρχήν ΞΥΠΝΗΣΤΕΕΕΕΕΕΕ και ακολούθως άμετε στο καλό του Μολώχ να πάμε και εμείς σπίτια μας.
Εσύ Τσιμπουκίδου ξέρεις, 6-8 μάθημα ε..
Αναρτήθηκε από Estarian στις 11:35 πμ
19 σχόλια:
Eleni είπε…
Lovely! Πού πήγε ο Chebyshev;
¨-)
12:23 μμ
i-fallos (Καπεταν Ηρεμος) είπε…
Εικασία του ifallos:
Είσαι και ο “πρώτος”!
@eleni
Άφησε ανοικτό ερώτημα ο Chebyshev? Γράψε κάτι παραπάνω!
1:39 μμ
Estarian είπε…
Ι-φαλλε, ρε συ, να αναδημοσιεύσουμε εδώ πέρα την εργασία του κλαπανάρα που ανταπέδειξε το πυθαγόρειο?? 🙂
1:53 μμ
Eleni είπε…
¨-) Μα ο Chebyshev δεν το άνοιξε το ερώτημα; Και ο Riemann δεν το “έκλεισε”;
Κι εδώ κάτι παραπάνω;
Νομίζω ότι για το 2005, από σχόλια blog κλείσαμε. Εξάλλου εσείς είστε οι ειδικοί.
…και γράφετε και lovely-ly.
🙂
2:01 μμ
i-fallos (Καπεταν Ηρεμος) είπε…
Αν αναλάβεις να προλογίσεις κατάλληλα, ώστε να αναδειχθεί το “μεγαλείο” της σκέψης!!!
Άλλωστε πιο “χαμένος” απ’ αυτόν δεν είναι κανένας μας. χε, χε, χε
2:49 μμ
Hugin είπε…
http://www.eff.org/awards/coop.php .
Για όποιον λέει οτι τα μάθηματίκα δεν έχουν φράγκα ή αλλιως βρείτε τον πρώτο και χέστειτε στο τάληρο :Ρ
2:55 μμ
Hugin είπε…
Α ναι και μιας και ανάφερθηκε η κρύπτογραφια ,ένα καλό begginer’s guide στα έλληνικα είναι το Τέχνικές κρύπτογραφίας και Κρύπταναλυσης εκδόσεις Ζυγός και το κύριοτερο σε πρόσιτη τίμη (36ε) σε αντίθεση με το φτήνοτερο αγγλίκο που βρήκα που ήταν στα 65 :).
Σορρυ για το double post αλλα οτι θύμαμαι χαίρομαι …
2:59 μμ
Hugin είπε…
Για τον Chebyshev:Απόδειξε το θέωρημα του Joseph Bertrand:Άναμεσα σε έναν άριθμο και το δίπλασιο του ύπαρχει ένας πρώτος άριθμος (δεν θυμάμαι αν είναι τουλάχιστον ένας η ένας).
Έπισης έθεσε το εξής:Αν διαίρεσεις έναν πρώτο αρίθμο με το 4 (πέραν του 2) το ύπολοιπο θα είναι είτε 1 είτε 3 .Μάλιστα οι άριθμοι 3mod4 είναι πάντα πέρισοτεροι απο τους 1 mod4 ( αύτο όνομαζεται Chebyshev bias ή η πρόκαταληψη του Chebyshev [δίκια μου μέτραφραση :Ρ ] ).Αύτο έχει απόδειχτει οτι ισχύει μέχρι τον ρ=26,861.
Αντίστοιχα αν διαίρεθει ένας πρώτος με το 3 το ύπολοιπο θα είναι είτε 1 είτε 2 και το bias είναι στο 2.Αύτο ίσχυει μέχρι το ρ=608,981,813,029.
3:38 μμ
Alberich είπε…
Το θεώρημα του Φερμά το απέδειξε ο Andrew Wile.Ο Wilson μάλλον άλλος είναι 🙂
Κάποιος φίλος εδώ είχε ξαναανακαλύψει-χωρίς να το ξέρει-ότι:
Κάθε πρώτος (πλην των 2 & 3) έχει τη μορφή 6ν+1 ή 6ν-1, χωρίς να ισχύει ότι κάθε αριθμός αυτής της μορφής είναι πρώτος.
7:08 μμ
Tero είπε…
Andrew Wiles και όχι Wilson…
(Μια φορά το 1 δεν θεωρούταν πρώτος αριθμός;)
Tero
12:44 πμ
Hugin είπε…
To θεώρημα του Wilson:Ο φύσικος ρ>2 είναι πρώτος ανν (ρ-1)==-1(modp)(όπου == ίσοτιμο ) .
2:29 πμ
i-fallos (Καπεταν Ηρεμος) είπε…
Μ’ αρέσει που σιγά σιγά γινόμαστε πολλοί!
4:59 μμ
Estarian είπε…
Συγγνώμη για το ατόπημα στο όνομα του Wiles, αλλά ένα μυαλό το χουμε.. 🙂
3:05 μμ
Estarian είπε…
Α και, Hugin και λοιπά συναδέλφια, ας προσπαθούμε ρε παιδιά να γράφουμε όσο απλούστερα γίνεται για να χαμπαριάζει και ο κόσμος που δεν έχει σπουδάσει μαθηματικά οκ? 🙂 Αμα είναι να τα λέμε μόνο για μας, είναι δώρο άδωρο 🙂
3:07 μμ
mikesmith58152498 είπε…
i thought your blog was cool and i think you may like this cool Website. now just Click Here
2:09 μμ
christos είπε…
Πρώτος ο καθηγητής….. Πρώτη και η Τσιμπουκίδου (στο είδος της)
2:56 μμ
vasvoe είπε…
Ωραίο μπλογκ έχετε παιδιά, μπράβο σας!
Να μαθαίνω τίποτα κι εγώ η άσχετη! Καλά να μαθαίνω λίγο δύσκολο με το μυαλό μου το τρύπιο, αλλά τουλάχιστον κάτι να έχει πάρει το αυτί μου!
9:08 μμ
Furure_Mathematician_89 είπε…
Καλημέρα σ’ όλη την παρέα!
Μια ερώτηση έχω:
“Είναι φύσην δυνατόν να σας παρακολουθήσει ένας normal μαθητής 2ρας Λυκείου, ή να το αναβάλλω για μερικά χρονάκια, μεχρι δηλ. να βγάλω άσπρα μαλλιά και γένια”? 😛
Y.Γ: Αν ειναι δυνατόν, προτηνετέ μου ορισμένα sides όπου μπορώ να αποκτήσω ορισμένες “στοιχειώδης” ιστορικές γνώσεις πάνω στα Μαθηματικά
3:03 μμ
Spiros είπε…
Hugin είπε…
Για τον Chebyshev: Απόδειξε το θέωρημα του Joseph Bertrand: Άναμεσα σε έναν άριθμο και το δίπλασιο του ύπαρχει ένας πρώτος άριθμος (δεν θυμάμαι αν είναι τουλάχιστον ένας η ένας).
Δεν είναι μόνο ένας επειδή ανάμεσα στο 4 και στο 8 υπάρχουν δύο, το 5 και το 7, όπως και στο 6 με 12 υπάρχουν το 7 και το 11.
1:42 πμ